FLOW-3D泥沙输移模型

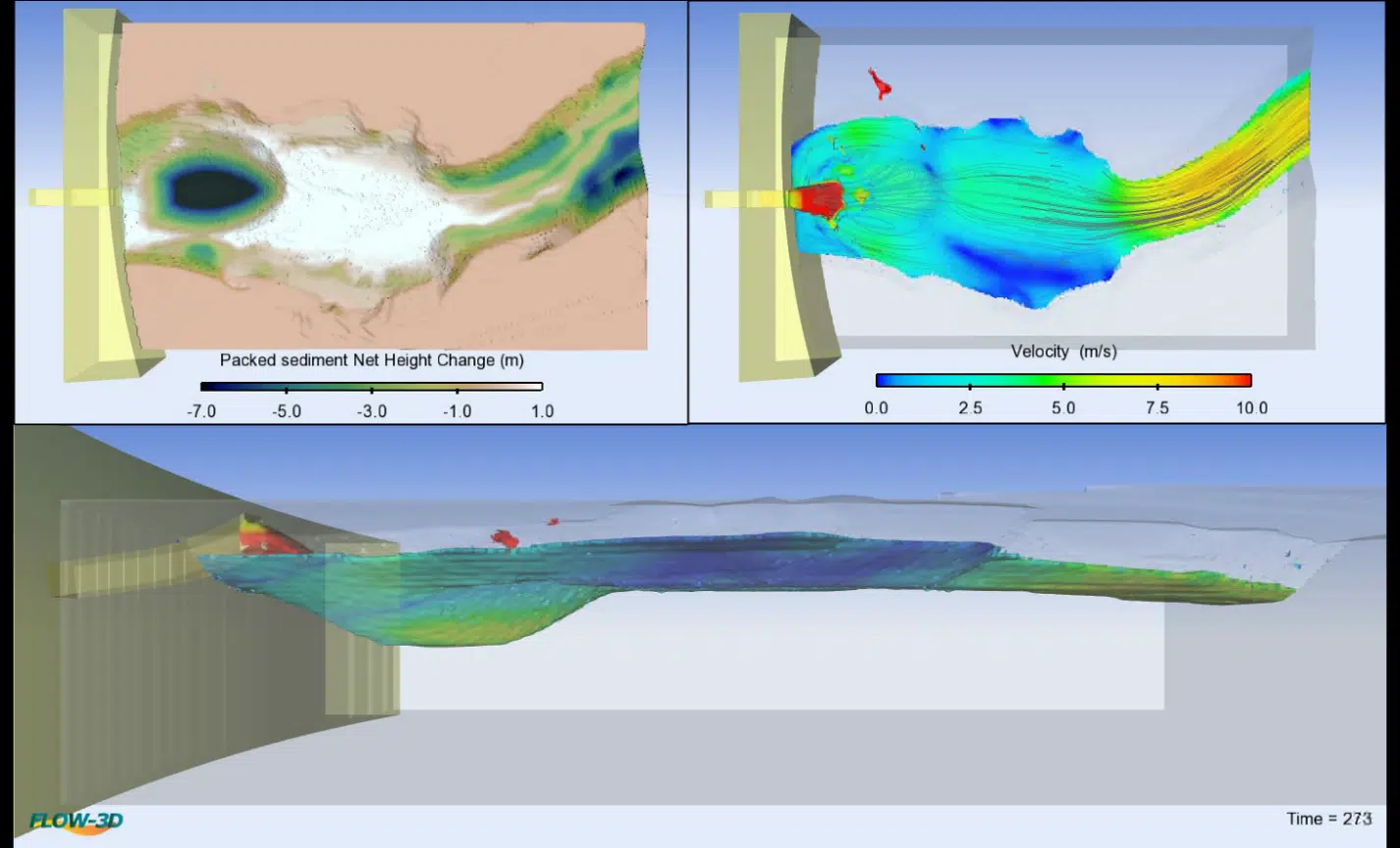
FLOW-3D的泥沙输移模型可用于评估冲刷和沉积。FLOW-3D的流体动力学模型求解完整的非定常的雷诺平均 Navier-Stokes 方程。水动力求解器与泥沙输移模型完全耦合,模拟非粘性推移质和悬移质输移、夹带和侵蚀(Wei et al., 2014)。推移、夹带和沉降过程中使用的所有经验关系都是完全可定制的,并且可以定义多达 10 种不同的泥沙种类(具有不同的特性,例如粒度、质量密度和临界剪切应力)。 FLOW-3D 非常适合模拟瞬时局部冲刷。
|
建模能力
|
应用
|
泥沙输移模型
泥沙输送模型在 8.0 版(Brethour,2009 年)中首次引入,并在 11.1 版(Wei 等人,2014 年)和最近的 12.0 版(Flow Science,2019 年)中进行了广泛的修订。数值模型中模拟的物理过程示意图如下所示。
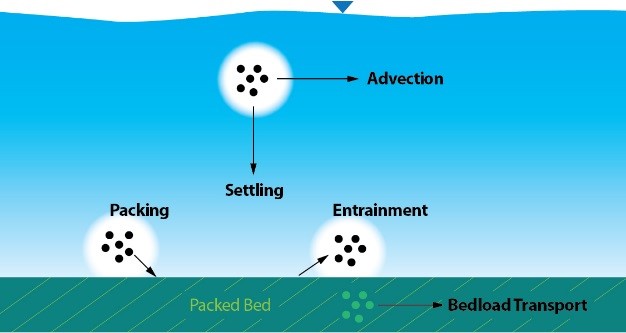
 由泥沙输移模型建模的不同过程。
由泥沙输移模型建模的不同过程。
在数值模型中,泥沙可以以推移质和悬移质存在。推移质是一种可侵蚀的固体物体,使用 FAVOR™ 技术表示复杂的固体边界(Hirt 和 Sicilian,1985 年)。这与在流体动力学求解器中用于表示实体对象的方法相同。推移质的形态变化受泥沙质量守恒控制。
推移质形态变化受几个不同物理过程的控制。这些过程包括推移质输移、夹带和沉积。推移质输移是泥沙沿河道横向移动而不被带入悬浮液的物理过程。夹带是湍流涡流将颗粒从推移质顶部移出并转变为悬移质的过程。包装是谷物从悬浮液中沉淀出来并沉积到推移质上的过程。在数值模型中,这是从悬浮床状态到推移质状态的转变。
夹带和沉积的相对速率控制推移质和悬移质之间的泥沙质量交换。该模型使用 Meyer-Peter Müller (1948)、Nielsen (1992) 或 Van Rijn (1984) 的方程计算包含沙床界面的每个网格单元中的推移质输移。采用子网格方法来确定从网格单元移动到其相邻网格单元中的每个网格单元的泥沙颗粒数量。使用 Winterwerp 等人的方程计算夹带中颗粒的卷带速度。(1992)。沉降速度是使用 Soulsby (1997) 计算的。在包含沙床界面的网格单元中,计算界面的位置、方向和面积,以确定沙床剪切应力、无量纲剪切应力、推移质输移速率和夹带速率。
悬移质表示为流体中的标量质量浓度。假定给定单元中的浓度是均匀的,并与流体单元的密度和粘度相结合。对于每种泥沙,通过求解输运方程计算悬移质浓度。
验证
以下五个验证案例将实验数据与FLOW-3D的泥沙输送模型的模拟结果进行比较。
Mao(1986)
Mao进行了实验工作,以获得水下水平管道下方的河床侵蚀冲刷剖面。下图将使用 FLOW-3D获得的结果与实验结果进行了比较。

图 A 比较了管道下的最大冲刷深度随时间的变化,而图 B 到 F 将研究中的冲刷剖面(显示为红点)与FLOW-3D中的冲刷剖面重叠。
Chatterjee et al. (1994)
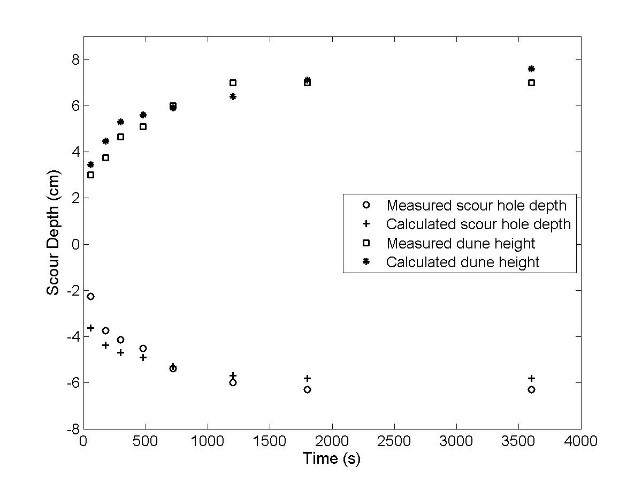
由于水下水平射流,进行了实验工作以获得局部冲刷剖面。下图比较了时间函数的冲刷坑深度和砂丘高度的实验结果与 FLOW-3D的数值结果。动画显示冲刷坑和砂丘高度在约 1 小时内达到稳定状态。
Gladstone et al.(1998)
在这些实验中,研究了悬移质的输移和沉积模式。下图比较了三种不同设置的实验与FLOW-3D模拟结果,标记为案例 A(100% 0.025 毫米大小的颗粒)、案例 D(50% 0.069 毫米和 50% 0.025 毫米大小的颗粒)和案例 G(100% 0.069 毫米大小的颗粒)。
Faruque et al. (2006)
在本文中,通过试验研究了水下三维壁面射流的局部冲刷。下表比较了三种不同尾水比率下冲刷孔中 3D 形态变化的实验与FLOW-3D数值结果。

圆柱桥墩的数值模型预测的河床高程变化。(A) 桥墩附近冲刷和沉积的等距图。(B) 数值结果(顶部)和物理模型测量结果(底部)之间的比较。
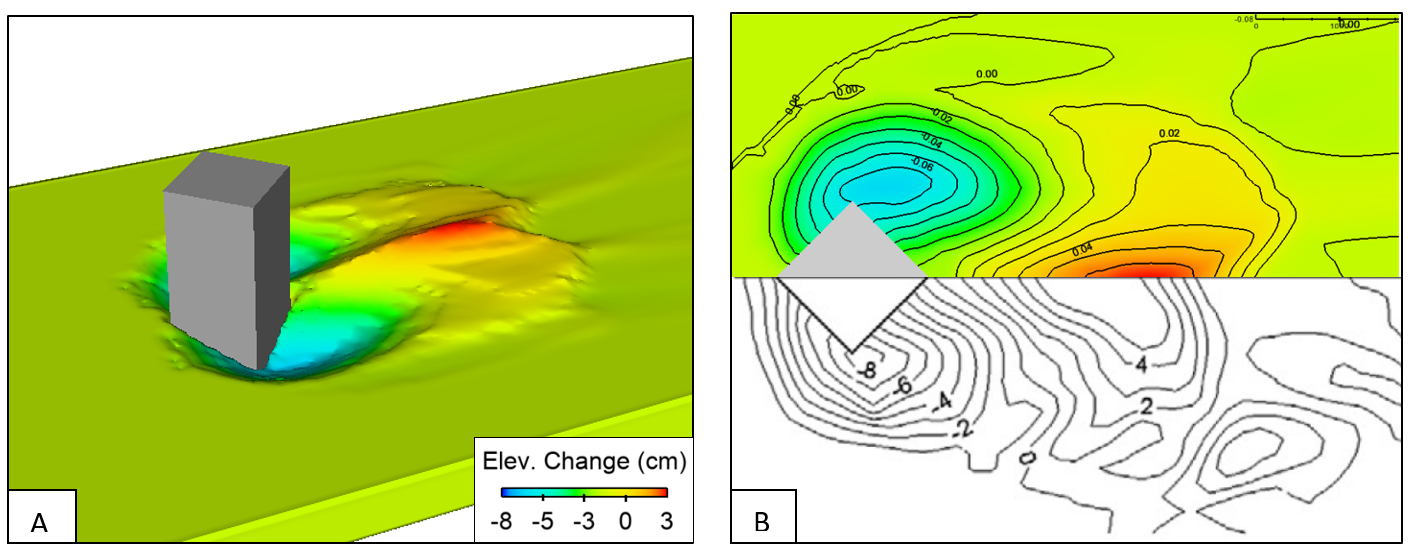
金刚石桥墩数值模型预测的河床高程变化。(A) 桥墩附近冲刷和沉积的等距图。(B) 数值结果(顶部)和物理模型测量结果(底部)之间的比较。
更多信息关注公众号:


参考文献
- Brethour, J.M., Hirt, C.W., 2009, Drift Model for Two-Component Flows, FSI-14-TN-83, Flow Science, Inc.
- Chatterjee, S.S., Ghosh, S.N., and Chatterjee M., 1994, Local scour due to submerged horizontal jet, Journal of Hydraulic Engineering, 120(8), pp. 973-992.
- Faruque, M.A.A., Sarathi, P., and Balachandar R., 2006, Clear Water Local Scour by Submerged Three-Dimensional Wall Jets : Effect of Tailwater Depth, Journal of Hydraulic Engineering, 132(6), pp. 575-580.
- Flow Science, 2019, FLOW-3D Version 12.0 User Manual, Santa Fe, NM: Flow Science, Inc. https://www.flow3d.com
- Fox, B. and Feurich, R., 2019, CFD Analysis of Local Scour at Bridge Piers, Federal Interagency Sedimentation and Hydrologic Modeling Conference (SEDHYD), Reno, NV.
- Gladstone, C., Phillips, J.C., and Sparks R.S.J., 1998, Experiments on bidisperse, constant-volume gravity currents: propagation and sediment deposition, Sedimentology 45, pp. 833-843.
- Hirt, C.W. and Sicilian, J.M., 1985, A porosity technique for the definition of obstacles in rectangular cell meshes, 4th International Conference on Numerical Ship Hydrodynamics, Washington, D.C.
- Khosronejad, A., Kang, S., & Sotiropoulos, F., 2012. Experimental and computational investigation of local scour around bridge piers, Advances in Water Resources, 37, pp. 73-85.
- Mao, Y., 1986. The interaction between a pipeline and an erodible bed, PhD thesis, Institute of Hydrodynamics and Hydraulic Engineering, Technical University of Denmark, Lyngby, Denmark.
- Meyer-Peter, E. and Müller, R., 1948, Formulas for bed-load transport, Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research. pp. 39–64.
- Nielsen, P., 1992, Coastal bottom boundary layers and sediment transport (Vol. 4). World scientific.
- Soulsby, R., 1997, Dynamics of Marine Sands, Thomas Telford Publications, London.
- Van Rijn, L. C., 1984, Sediment Transport, Part I: Bed load transport, Journal of Hydraulic Engineering 110(10), pp. 1431-1456.
- Wei, G., Brethour, J.M., Grüenzner M., and Burnham, J., 2014, The Sediment Scour Model in FLOW-3D, Technical Note FSI-14-TN-99, Flow Science, Inc.
- Winterwerp, J.C., Bakker, W.T., Mastbergen, D.R. and Van Rossum, H., 1992, Hyperconcentrated sand-water mixture flows over erodible bed, Journal of Hydraulic Engineering, 118(11), pp. 1508–1525.



